Energy Efficiency
Intro
Lecture draws on:
Allcott and Greenstone (JEP 2012)
Allcott (Annual Review 2014)
Gerarden, Newell and Stavins (JEL 2018)
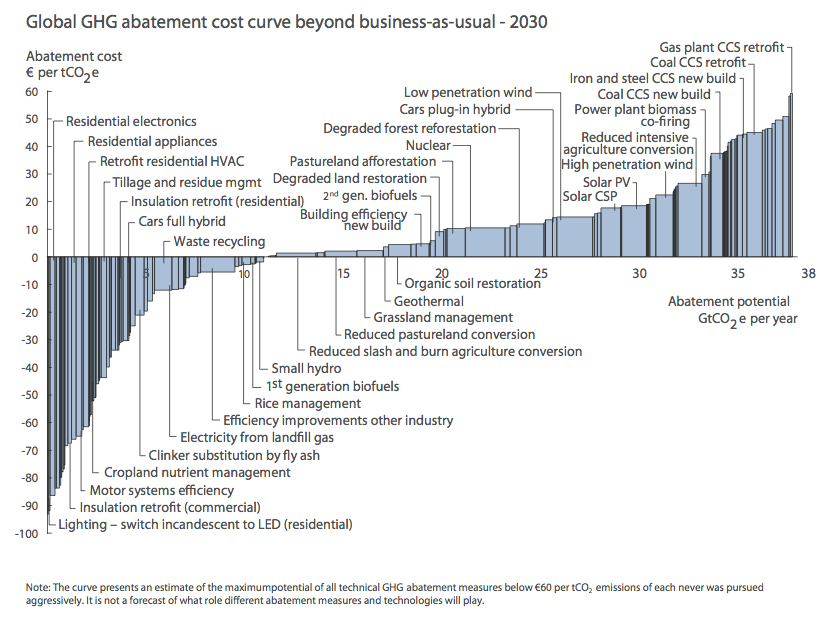
Energy services require capital
Source: Allcott and Greenstone (2012)
Long standing assertion that energy efficient capital suboptimally deployed
-
Serious interest began during oil crisis in 1970s
-
Engineers concluded that many energy saving technologies were slow to diffuse
- for example Amory Lovins and RMI
Over time interest has centered on apparent "win-win" from environmental perspective
- Energy consumption associated with many externalities
40 years later this view still has a large audience
There are many "rational" reasons for EE gap
-
agency issues
- ie landlord tenant
-
resale issues
- home improvements
-
engineering models wrong
- Fowlie, Greenstone and Wolfram (QJE 2018)
Research focussed on "behavioral" explanations
-
[present bias]
- tradeoff is over cash flows not consumption
- car or mortgage payments also flows
- firm mispricing problem less clear
- car companies don't sell you gasoline
- tradeoff is over cash flows not consumption
-
inattention/ salience
- Chetty et al (2009); Hossain & Morgan (2006)
-
cognitive issues /confusion
- Abaluck & Gruber (2011); Allcott (2013)
Setup
Consumers have indirect utility
- $p_j$ is upfront cost
- $\nu_j$ is the usage utility
- $g_j$ is the lifetime energy cost
Assuming $g$ is calculated and discounted appropriately, a natural test is to estimate $\gamma$ and test if its equal to 1.
Lifetime energy costs
- $m$ is utilization
- $r_j$ is energy requirement for capital $j$
- $e$ is the energy price
Note
- $\delta, m, T, e$ could all have $i$ subscripts
- if $m$ is endogenous, can lead to a "rebound effect"
Early literature tried to estimate $\delta_i$
Hausman (1979) estimates a discrete choice model for AC's
- Has a small survey of households with submetered ACs
Literature then turned to within product variation
- In the cross section, concern that $E[r_j \epsilon_j] \ne 0$
However, $g_{ij}$ varies for many other reasons within product
- energy prices vary
- across regions, time
- lifetime varies at time of sale
- Sallee et al. look at mileage
Allcott and Wozny
- What's the research question?
- What's the empirical strategy?
- What data do they have?
AW cost to own
- used car auction vehicle prices from Manhiem
- what are the assumptions using this?
- assumed real discount rate of 6%
- vehicle loan rate 6.9%
- S&P avg return 5.9%
- (exogenous) VMT ($m$) and $T$ from NHTSA
- fuel economy from EPA
- national avg gasoline prices / oil futures
Controlling for product quality clearly matters
Identifying variation
AW use hedonic regression
Typical logit share identity (Berry, 1994):
AW actually estimate:
Why do they do this?
Berry equation rearranged is
- The don't have shares.
- Absorb $s_{ot}$ with time FEs.
- Put product FEs in $\psi_{ja}$
- $\xi$ and the remaining share difference in the $\epsilon$
- So this tests it tests whether relative vehicle prices move one-for-one with changes in the relative gasoline costs.
- Coeff of interest $\gamma$ recovered with OLS.
AW also using a grouping estimator
-
group all cars by month, above / below median
- $Z_{jat}^u = 1(f_{ja} > f^{50}) \times 1(t=u$)
-
instrument for $G$ with $Z$
-
why do they do this?
Jerry Hausman's (2001) "iron law of econometrics": due to measurement error, the magnitude of a parameter estimate is usually smaller in absolute value than expected
What is the null hypothesis that AW want to test?
Visual results
AW Results - Sensitivity
What do people takeaway from this paper?
-
tradeoff implies discount rate of about 15%
- for new cars, close to 1
- old cars, very low
-
results sensitive to how G is constructed
-
are people making mistakes?
-
what questions does this leave open?
Allcott and Knittel
Recent emphasis has been on experiments
-
Many studies similar to AW
-
Although panel data helps, interpretation still requires econometrician to construct $g$
-
If hypothesis is that $\gamma < 1$ due to inattention, imperfect information or bounded rationality, an alternative is to experimentally vary exactly those margins
Alternative: AK 2019 conduct two large field experiments
Experiment #1:
- Hang out at car dealers and intercept potential buyers
- Randomly explain fuel economy savings to some
Experiment #2:
- Conduct and online survey of people how say they are in the market for a new car
- In addition to following up on what people actually bought, AK elicit WTP for fuel economy.
Some advantages of surveys
-
can ask people about consideration sets
-
can ask about beliefs
-
can elicit WTP
Consideration sets reveal important differences
Beliefs about fuel costs noisy, but not biased
Results
Policy Implications

Some conclusions from core EE gap lit
-
assertion that consumers making large mistakes on average appears incorrect
-
once you account for product unobservables and use exogenous fuel cost variation, tradeoffs seem close to rational
-
experimental studies directly educating or directing consumer attention to energy costs have found very small impacts
Future directions
-
Heterogeneity in both values and bias
- policy implications
- targeting
-
What role do firms play here?
- Are they offering the "right" set of products?
-
How do consumer's form beliefs?
- we know the true calculation is hard
- rational inattention (Sallee JLE 2014)
- we know the true calculation is hard
Allcott and Taubinsky
Can policymakers improve welfare in this market?
-
develop a theoretical framework in presence of heterogenous bias and tastes
-
implement two experiments informing consumers about CFLs
-
evaluate welfare effects:
- optimal subsidy
- [ban on incandescents]
Corrective taxation with damage heterogeneity
Pigou (1920):
If damages are heterogenous, first best achieved with polluter specific tax
Diamond (BJE 1973): If damages are heterogeneous, but you can only set one tax rate, it should be equal to the average damages at the margin when the tax is implemented.
AT show this also applies to correcting biases
Setup
-
unit demand: $j \in {E,I}$
- no outside option
-
utility: $u_j = v_j + z - P_j$
- where $z$ is the consumer's budget
-
choose $E$ if $v - b > p$
- $v = v_E - v_I$
- $b$ is bias
Demand with and without bias
Welfare effect of subsidy
- perfect competition: $p = c - s$
Proposition 1:
where $B = E(b|v - b = p)$ is the average marginal bias -- ie the average bias for consumers on the margin the (subsidized) price
Optimal subsidy:
Average Marginal Bias
AMB is the key object of policy interest
Need not be constant
- Average marginal bias $\ne$ average bias
How can we estimate the average marginal bias?
Option 1:
- use within consumer variation in informedness
Option 2:
- estimate demand elasticity wrt tax and information
- calibrate difference
TESS experiment
-
Artefactual field experiment
-
Give consumers $10
-
Elicit WTP ($v$) for CFLs
-
Inform some consumers about cost to own to recover $b$
Many papers have used TESS
Informed vs uninformed demand
Average marginal bias not constant
Welfare effects
Welfare effects
Allcott, Knittel and Taubinsky
Extend AT model to allow correlation in bias and valuation
-
consumers of type $j$ have distortions $d$ (nests bias from AT)
- value $v - d$
-
population average $\bar d = \sum \alpha_j d_j$
-
define targeting as:
$$\tau (s) \equiv cov ( d_j, -Q'_j(c-s) )$$- so a high $\tau(s)$ is well "targetted"
Welfare and optimal subsidy
Result 1:
Poor targeting reduces welfare gains
Result 2:
Optimal poorly targeted subsidy could be small, even if average bias is large
[ Optimal subsidy increasing in $\tau(s)$ ]
Bias is correlated with observables
As is policy takeup
Where does this leave us?
-
Optimal subsidy depends on average marginal bias
-
Not sufficient to know bias and responsiveness separately: need to show biased consumers are actually the onces affected by the policy.
Allcott and Sweeney
What we did
- partner with major appliance retailer
- field experiment at call center
- customer information and rebates
- sales agent incentives
- audit phone calls to check compliance
- survey consumers
Some thoughts on running a field experiment
-
getting institutional buy in was tough
- in end, partner lost interest
-
compliance a big issue
- has implications for feasible policy too
Some agents much better than others
Survey reveals widespread confusion, but small bias
Main Results
Agents Target Scripts
What role do firms play in this?
-
Allcott & Sweeney: Sales agents can target. Can we leverage this somehow?
-
Houde (2014): firms bunch product characteristics around subsidy / label cutoffs
-
Houde (2018): labeling may further reduce average purchased quality